#hide_input
import torch
import torch.nn as nn
import numpy as np
import tensorflow as tf
import pandas as pd
from sklearn.metrics import accuracy_scoreIn this post we will be going over the intuition, theory and implementation of a gated RNN, particularly LSTM. This is the sequel to my previous post about RNNs.
Note: This post builds on my previous explanation of RNNs. The dataset used in this post is the IMDB dataset of 50,000 movie reviews, used for sentiment classification.
RNN vs LSTM
LSTM, shorthand for Long-Short-Term-Memory, is a recurrent architecture for processing sequences just as the vanilla RNN. Compared to LSTM, the vanilla RNN is not used in practice as much, as it has some notable limitations that the LSTM architecture tries to address. These include:
- Exploding/Vanishing Activations
- Memory Limitations
Exploding/Vanishing Activations
The problem of exploding/vanishing gradients occurs due to the way the vanilla RNN backpropagates gradients. If you consider the unrolled representation of an RNN and its backpropagation mechanism you will quickly notice that for long sequences there is a lot of repeated multiplication done in order for gradients to arrive from the last layer to the initial one. This is the exact reason why we might experience exploding/vanishing gradients. Let’s explore this problem in more detail by simulating repeated multiplication in a backpropagation.
Let say we have a sequence of length 50. We will multiply matrices initialized with random numbers from a normal distribution.
x=torch.randn(50,50)
for i in range(50):
x= x @ torch.randn(50,50)
xtensor([[nan, nan, nan, ..., nan, nan, nan],
[nan, nan, nan, ..., nan, nan, nan],
[nan, nan, nan, ..., nan, nan, nan],
...,
[nan, nan, nan, ..., nan, nan, nan],
[nan, nan, nan, ..., nan, nan, nan],
[nan, nan, nan, ..., nan, nan, nan]])This is the occurence of exploding gradients. Basically, our numbers got so large that it caused numerical overflow and produced NaNs. What if we try to mitigate this by decreasing our matrices by a factor of 0.01?
x=torch.randn(50,50)
for i in range(50):
x= x @ torch.randn(50,50)*0.01
xtensor([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]])Now, this produced vanishing gradients or numerical underflow. The numbers became so small that our computer just represents them with zeros. If we would have a weight matrix like this in any part of our neural network it would break the models learning capability, so that is why this is a delicate but important problem to solve.
Solutions to this include: - Identity initialization of weights paired with ReLU activation - Gradient clipping - Skip connections - Model alteration
LSTM is an instance of a model approach to this problem. It mitigates the vanishing/exploding gradients problem by introducing the concept of gates which change the way gradients flow.
Memory Limitations
If you would experiment with RNNs, e.g. for next-word-prediction (language model), you would notice that they have a hard time with long-term memory needed in sentences such as this:
“I grew up in France and had a wonderful childhood, therefore I speak fluent French” -The language model would need to retain the information of “France” until its useful for predicting the word “French”.
LSTMs do a much better job with long-term memory because of several reasons:
- An additional state called the cell state which enables accumulation of information over a long duration.
- The concept of memory management depending on the current timestep’s input and hidden state.
Cell State
LSTMs have an additional state called the cell state which is passed along with the hidden state to each cell. But the cell state has no linear layers through which it passes, therefore enabling easier information flow over a longer duration. This is what enables the long-term memory of an LSTM. Cell state is only influenced by element-wise operations controlled by gates which we will observe soon.
Memory Management
The term “gated RNN” comes from the fact that the cell state is gated (protected) by so-called gates. These gates are linear layers responsible for managing the cell state by extracting relevant information from the current timestep input and hidden state. The idea is that at each timestep the cell state information we don’t need anymore should be forgotten and new valuable information should be stored. Since these gates are layers we delegate this mechanism for the neural network to learn itself without us having to manage it manually.
Architecture
This is what the LSTM Cell looks like:
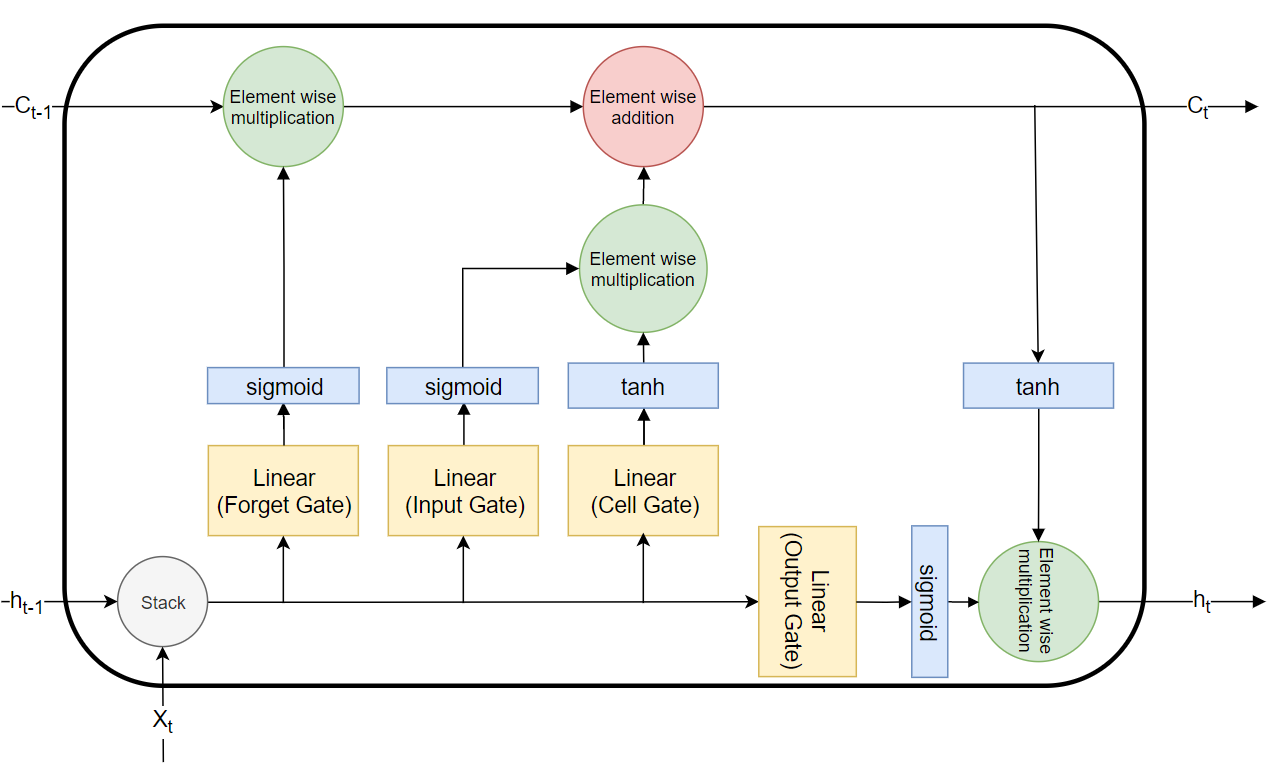
There are four gates and each of them is fed the stacked tensor of the current timestep’s hidden state and input. In summary, what each gate does for a sequence at a particular timestep is the following:
- Forget gate: what information to keep and what to forget in the long memory
- Input gate: what information needs to be updated in the long memory
- Cell gate: how the information will be updated in the long memory
- Output gate: what part of the long memory is relevant for the short memory
Forget Gate
Forget gate decides what to forget/eliminate from the cell state. It is followed by a sigmoid function, mapping values to the (0, 1) range. We then multiply this output element-wise with the cell state. If the scalar at some position of the sigmoid output is closer to 0 it will result in the elimination of the value at the same position in the cell state. The opposite is true for values close to 1.
Input Gate and Cell Gate
Input and Cell gate together decide what to update/store in the cell state. Input gate decides what needs to be updated and to what degree, dictated by the sigmoid. Cell gate decides what are the updated values for positions chosen by the input gate. Cell gate is followed by the tanh function mapping values to (-1, 1) range. The output of the input and cell gate is multiplied element-wise and then added element wise to the cell state.
Output Gate
Output gate decides which information from the cell state is relevant for the next hidden state. Then this is fed to the sigmoid and the output is multiplied element-wise with the tanh of the updated cell state
Implementation
Below is a PyTorch implemenation of the LSTM Cell we described.
class LSTMCell(nn.Module):
def __init__(self, n_input, n_hidden):
super(LSTMCell, self).__init__()
self.forget_gate = nn.Linear(n_input+n_hidden, n_hidden)
self.input_gate = nn.Linear(n_input+n_hidden, n_hidden)
self.cell_gate = nn.Linear(n_input+n_hidden, n_hidden)
self.output_gate = nn.Linear(n_input+n_hidden, n_hidden)
self.out=nn.Linear(n_hidden, n_hidden)
def forward(self, x, state):
h, c = state
h = torch.cat([h, x], dim=1)
forget_gate_out = torch.sigmoid(self.forget_gate(h))
input_gate_out = torch.sigmoid(self.input_gate(h))
cell_gate_out = torch.sigmoid(self.cell_gate(h))
output_gate_out = torch.sigmoid(self.output_gate(h))
c = c*forget_gate_out
c = c+(input_gate_out*cell_gate_out)
h = output_gate_out*torch.tanh(c)
out= torch.relu(self.out(h))
return out, (h, c)Note: This particular implementation is not efficient, its only a toy example. For an efficient implementation merge the 4 matrix multiplications into 1.
Hopefully, all parts of an LSTM are now clear. For an even better understanding continue to see it applied to sentiment analysis.
Performance
We will be testing LSTM’s performance on the IMDB dataset for sentiment analysis.
Preparing the dataset
# Loading data
data=pd.read_csv('./imdb.csv')
data=data.sample(frac=1)
print(data.head()) review sentiment
49390 I want to add to the praise for the production... positive
33574 A crackling and magnificent thriller about a c... positive
44801 Like most everyone who views this movie, I did... negative
379 I'm a big fan of surrealist art, but this film... negative
5305 This movie was the worst i've ever seen.<br />... negative# Splitting data
train=data[:25000]
xtrain=train['review'].values.tolist()
ytrain=train['sentiment'].values
val=data[25000:]
xval=val['review'].values.tolist()
yval=val['sentiment'].values
# Preprocessing (Tokenization and padding)
tokenizer=tf.keras.preprocessing.text.Tokenizer(num_words=3000)
tokenizer.fit_on_texts(xtrain)
xtrain_pro=tokenizer.texts_to_sequences(xtrain)
xtrain_pro=tf.keras.preprocessing.sequence.pad_sequences(xtrain_pro, maxlen=128)
xval_pro=tokenizer.texts_to_sequences(xval)
xval_pro=tf.keras.preprocessing.sequence.pad_sequences(xval_pro, maxlen=128)
ytrain=[1 if y=='positive' else 0 for y in ytrain]
yval=[1 if y=='positive' else 0 for y in yval]Now we create our dataset class and our datasets
class IMDBDataset:
def __init__(self,reviews,targets):
self.reviews=reviews
self.targets=targets
def __len__(self):
return len(self.reviews)
def __getitem__(self,idx):
review=self.reviews[idx,:]
target=self.targets[idx]
review=torch.tensor(review,dtype=torch.long)
target=torch.tensor(target,dtype=torch.float)
item=(review,
target)
return item
train_ds=IMDBDataset(xtrain_pro, ytrain)
val_ds=IMDBDataset(xval_pro, yval)Lastly, we create our dataloaders
train_dl=torch.utils.data.DataLoader(
train_ds,
batch_size=128,
)
val_dl=torch.utils.data.DataLoader(
val_ds,
batch_size=128,
)Constructing the SentimentClassifier Model with our LSTM
In order to apply the LSTMCell we package it in the LSTM class which applies it to a sequence.
class LSTM(nn.Module):
def __init__(self, n_input, n_hidden):
super(LSTM, self).__init__()
self.n_input = n_input
self.n_hidden = n_hidden
self.LSTMCell = LSTMCell(n_input, n_hidden)
def forward(self, input, state=None):
# Input dims are (batch_size, seq_length, timestep_features)
sequence_length = input.size()[1]
# Initialize hidden and cell state if not provided
if state == None:
h, c = (torch.zeros((input.size()[0], self.n_hidden), device=input.device),
torch.zeros((input.size()[0], self.n_hidden), device=input.device))
else:
h, c = state
outs = torch.tensor([], device=input.device)
for i in range(sequence_length):
x_timestep_features = torch.squeeze(input[:, i, :], dim=1)
out, (h, c) = self.LSTMCell(x_timestep_features, (h, c))
out = torch.unsqueeze(out, dim=1)
outs = torch.cat((outs, out), dim=1)
return outsFinally we package our LSTM into a SentimentClassifier class which uses an additional embedding layer and linear layer.
class SentimentClassifier(nn.Module):
def __init__(self,vocab_sz,n_hidden):
super(SentimentClassifier,self).__init__()
self.embedding=nn.Embedding(vocab_sz,n_hidden)
self.rnn=LSTM(n_hidden,n_hidden)
self.linear=nn.Linear(n_hidden*2,1)
def forward(self, x):
x=self.embedding(x)
x =self.rnn(x)
# Using the avg and max pool of all RNN outputs
avg_pool=torch.mean(x, dim=1)
max_pool, _ =torch.max(x,1)
# We concatenate them (hidden size before the linear layer is multiplied by 2)
out=torch.cat((avg_pool, max_pool), dim=1)
out=self.linear(out)
return torch.squeeze(out, dim=1)Constructing the training loop
device='cuda' if torch.cuda.is_available() else 'cpu'
device'cuda'model=SentimentClassifier(3000,100)
model=model.to(device)
loss_func=torch.nn.BCEWithLogitsLoss()
optimizer=torch.optim.Adam(model.parameters(), lr=1e-3)#hide
sigmoid= lambda x: 1 / (1+np.exp(-x))epochs=5
for epoch in range(epochs):
# Training
ys=[]
y_preds=[]
for x,y in train_dl:
x=x.to(device)
y=y.to(device)
y_pred=model(x)
loss=loss_func(y_pred,y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
ys.extend(y.detach().cpu().numpy().tolist())
y_preds.extend(y_pred.detach().cpu().numpy().tolist())
# Measuring Training accuracy
y_preds_final=sigmoid(np.array(y_preds))>0.5
accuracy=accuracy_score(y_preds_final,ys)
print(f"Epoch: {epoch} | Training accuracy: {accuracy:.2f}")
# Validation
ys=[]
y_preds=[]
with torch.no_grad():
for x,y in val_dl:
x=x.to(device)
y=y.to(device)
y_pred=model(x)
ys.extend(y.detach().cpu().numpy().tolist())
y_preds.extend(y_pred.detach().cpu().numpy().tolist())
# Measuring Validation accuracy
y_preds_final=sigmoid(np.array(y_preds))>0.5
accuracy=accuracy_score(y_preds_final,ys)
print(f"Epoch: {epoch} | Validation accuracy: {accuracy:.2f}")
print("-"*40)Epoch: 0 | Training accuracy: 0.66
Epoch: 0 | Validation accuracy: 0.75
----------------------------------------
Epoch: 1 | Training accuracy: 0.80
Epoch: 1 | Validation accuracy: 0.81
----------------------------------------
Epoch: 2 | Training accuracy: 0.85
Epoch: 2 | Validation accuracy: 0.84
----------------------------------------
Epoch: 3 | Training accuracy: 0.87
Epoch: 3 | Validation accuracy: 0.85
----------------------------------------
Epoch: 4 | Training accuracy: 0.89
Epoch: 4 | Validation accuracy: 0.85
----------------------------------------For the end we can test our model on arbitrary input.
#collapse-hide
def predict(model,text):
x=tokenizer.texts_to_sequences(text)
x=tf.keras.preprocessing.sequence.pad_sequences(x, maxlen=128)
x=torch.tensor(x,device='cuda')
model.eval()
with torch.no_grad():
logit=model(x)
prob=sigmoid(logit.cpu().numpy())
print(f"Output: {str(prob)} | ", end='')
if prob>=0.5:
print(f'Sentiment: positive')
else:
print(f'Sentiment: negative')text=['This guy made this blog about LSTMs and provided the implementation without explaining each line of the code!']
predict(model,text)Output: [0.2402171] | Sentiment: negative